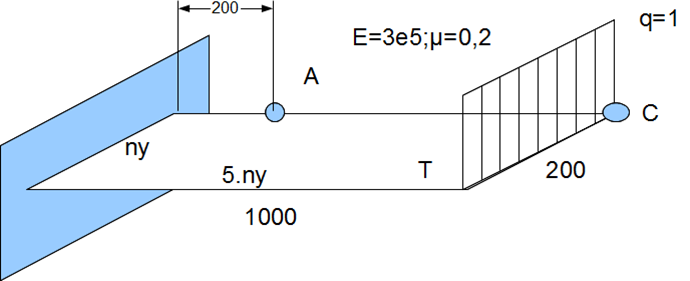
Bending of Quad 1
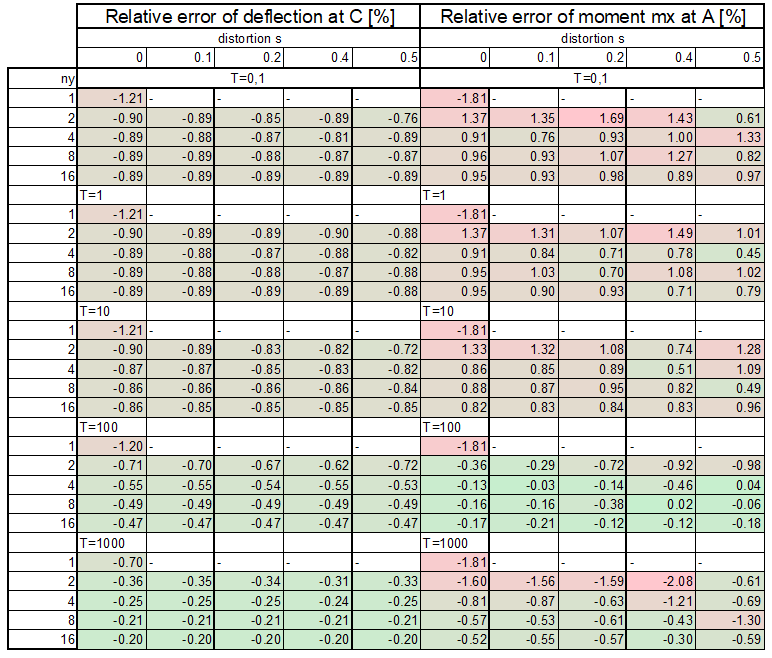
Theoretical results:
- Deformation at point C: \(w_c=0.096/T+13333.33333/T^3\)
- Bending moment at A: \(m_x=800\)
Distortion coefficient s of mesh is defined by moving all internal nodes by
\[x'=x+r_c s \Delta x\]
\[y'=y+r_c s \Delta y\]
where \(r_c\) is a random number in interval \(<-1, 1>\), \(\Delta x\) or \(\Delta y\) are typical element lengths.
Mesh examples:
Comparison of numerical and theoretical results:
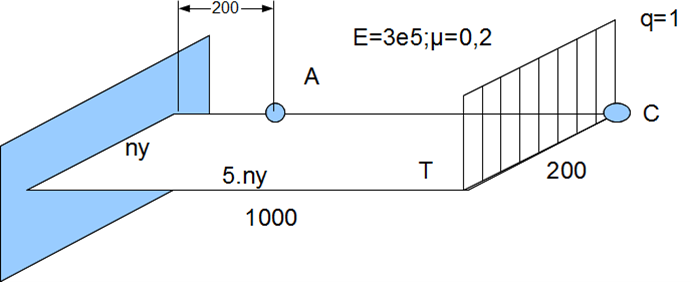
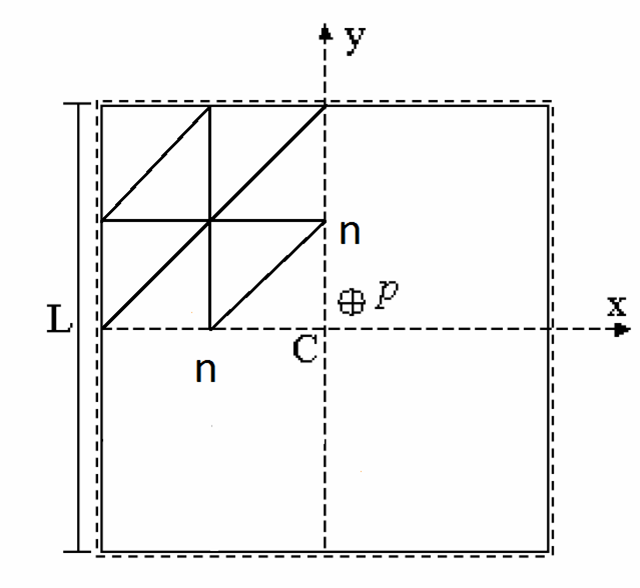
Bending of Tria 1
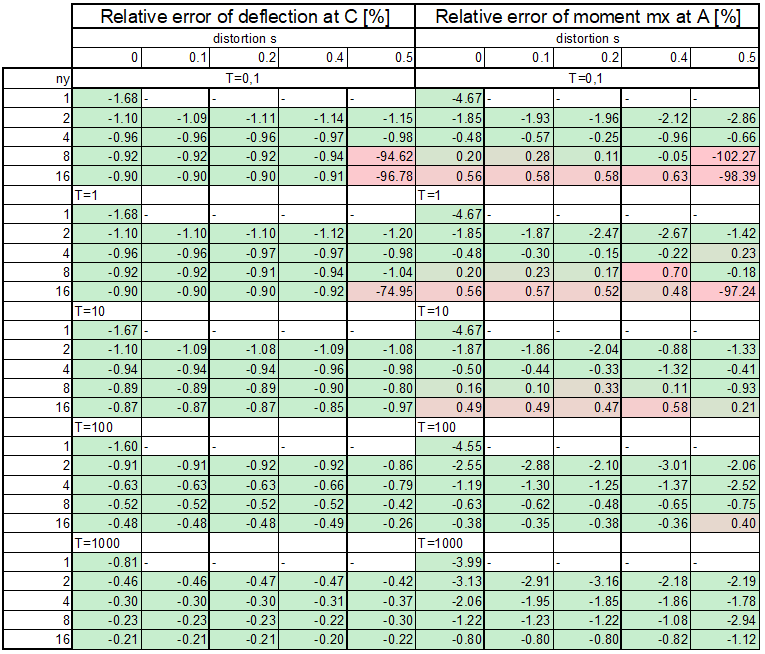
Theoretical results:
- deformation at point C: \(w_c = 0.096/T+13333.33333/T^3\)
- moment at A: \(m_x=800\)
Distortion coefficient s of mesh is defined as moving all internal nodes by
\[x'=x+r_c s \Delta x\]
\[y'=y+r_c s \Delta y\]
where \(r_c\) is a random number in interval \(<-1, 1>\), \(\Delta x\) or \(\Delta y\) are typical element lengths.
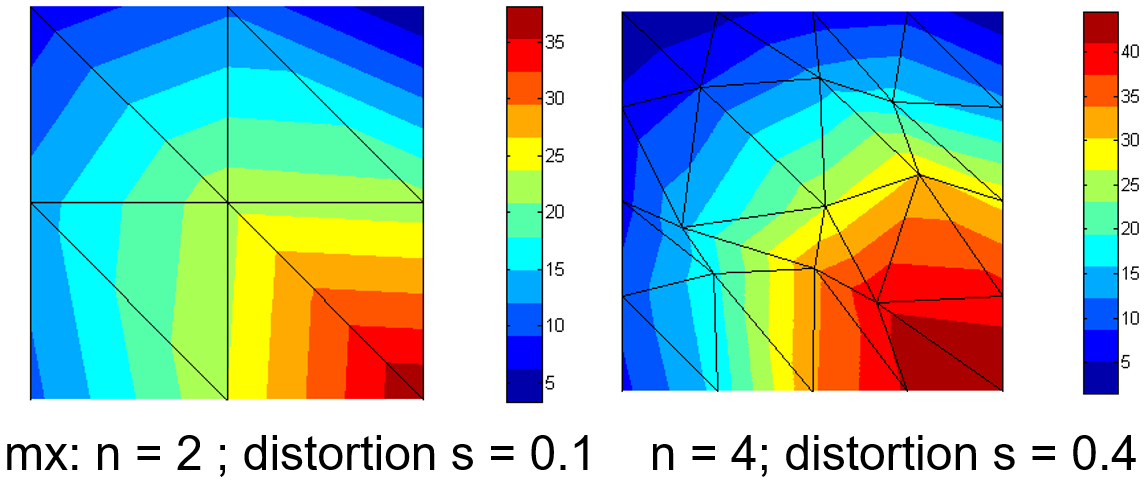
Mesh examples:
Comparison of numerical and theoretical results:
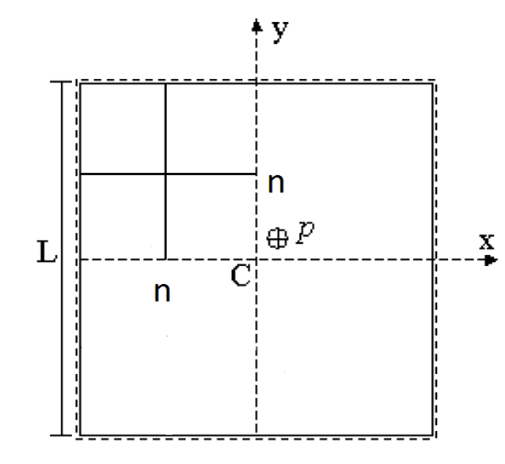
Bending of Quad 2
Simple supported square plate
\[L=1000;\,E=2.1e5;\,μ=0.3;\,p=1e-3\]
Theoretical solution (by sinus series expansion):
- Deflection at C: \(w_t = 211.2423380/T^3+0.1094543906e-2/T\)
- Bending moment \(m_x\) at C: \(m_{x,C} = 47.88629590\)
Distortion is defined as in the first benchmark.
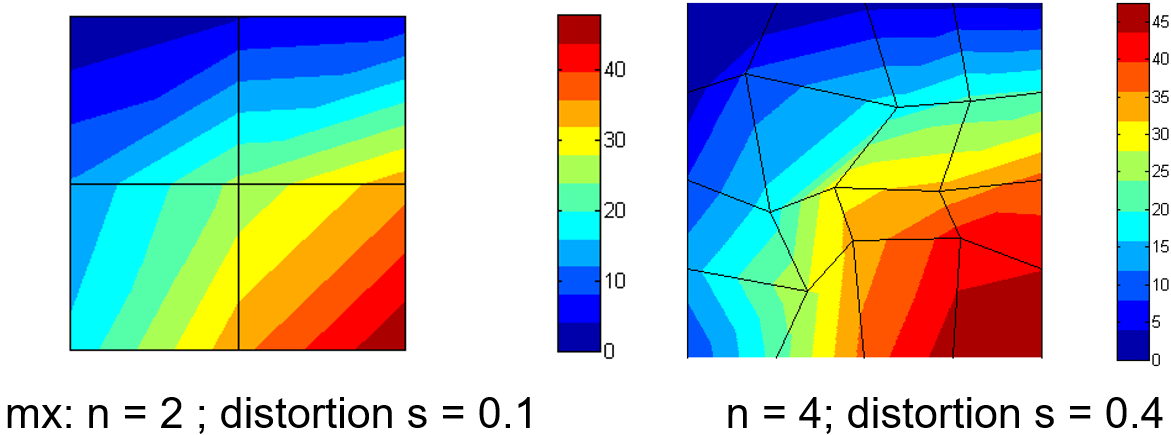
Mesh examples:
Comparison of numerical and theoretical results:
Bending of Tria 2
Simple supported square plate
\[L=1000;\,E=2.1e5;\,μ=0.3;\,p=1e-3\]
Theoretical solution (by sinus series expansion):
- Deflection at C: \(wt = 211.2423380/T^3+0.1094543906e-2/T\)
- Moment \(m_x\) at C: \(m_{x,C} = 47.88629590\)
Distortion is defined as in the first benchmark.
Mesh examples:
Comparison of numerical and theoretical results:
Conclusion
Generally, the convergence to analytical solution for plate bending is very fast. Quads do not have any issues even with a high distortion coefficient. Extreme distortion may be an issue for Trias; it is recommended to watch out for Tria elements with very bad aspect ratio. IDEA StatiCa Steel greatly prefers Quads in automatic meshing.
The results do not vary significantly for different thicknesses.