4.1.1 Description
The object of this chapter is verification of component based finite element method (CBFEM) of a fillet weld in a lap joint with component method (CM). Two plates are connected to each other in three configurations, i.e. with a transverse weld, with a longitudinal weld and combination of the transverse and longitudinal welds. The length and throat thickness of the weld are the changing parameters in the study. The study covers long welds, which resistance is reduced due to stress concentration. The joint is loaded by normal force.
4.1.2 Analytical model
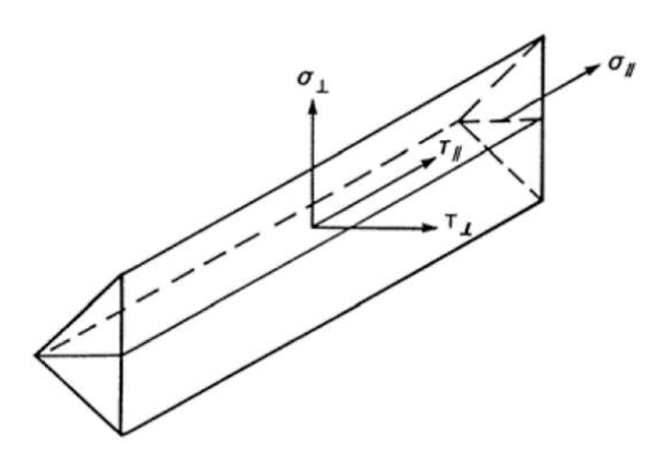
The fillet weld is the only component examined in the study. The welds are designed to be the weakest component in the joint. The weld is designed according to EN 1993-1-8:2005. The design resistance of the fillet weld is determined using the Directional method given in section 4.5.3.2 EN 1993-1-8:2005. The available calculation methods for checking the strength of fillet welds are based upon the simplifying assumption that stresses are uniformly distributed within the throat section of a fillet weld. A uniform distribution of stress is assumed on the throat section of the weld, leading to the normal stresses and shear stresses shown in Fig. 4.1.1, as follows:
σ┴ is the normal stress perpendicular to the throat section;
σ║ is the normal stress parallel to the axis of the weld on its cross section;
τ┴ is the shear stress (in the plane of the throat section) perpendicular to the axis of the weld;
τ║ is the shear stress (in the plane of the throat section) parallel to the axis of the weld.
The normal stress σ║ parallel to the axis is not considered when verifying the design resistance of the weld.
Fig. 4.1.1 Stresses on the throat section of a fillet weld
The design resistance of the fillet weld will be sufficient if the following are both satisfied:
Fig, 4.1.2 Joint’s geometry with dimensions
a) Transverse weld b) Parallel weld c) Combination of transverse with parallel weld
4.1.3 Numerical model
The weld component in CBFEM is described in Chapter 3.4. Nonlinear elastic-plastic material is used for welds in this study. The limiting plastic strain is reached in longer part of the weld and stress peaks are redistributed.
4.1.4 Verification of resistance
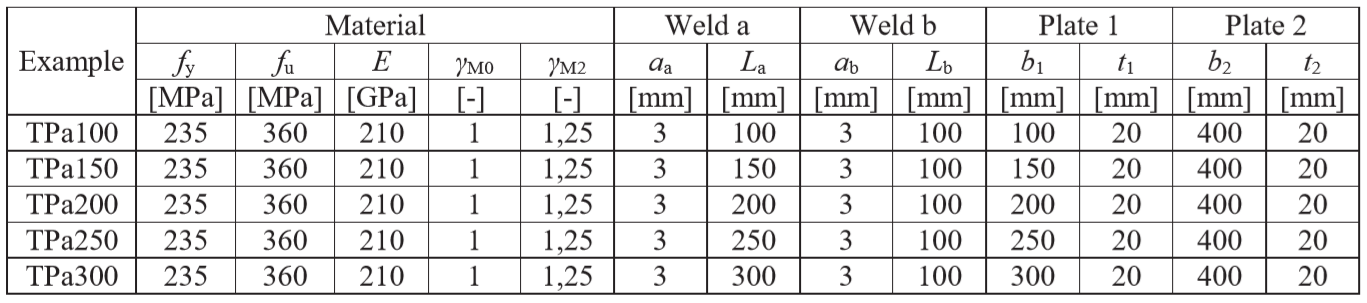
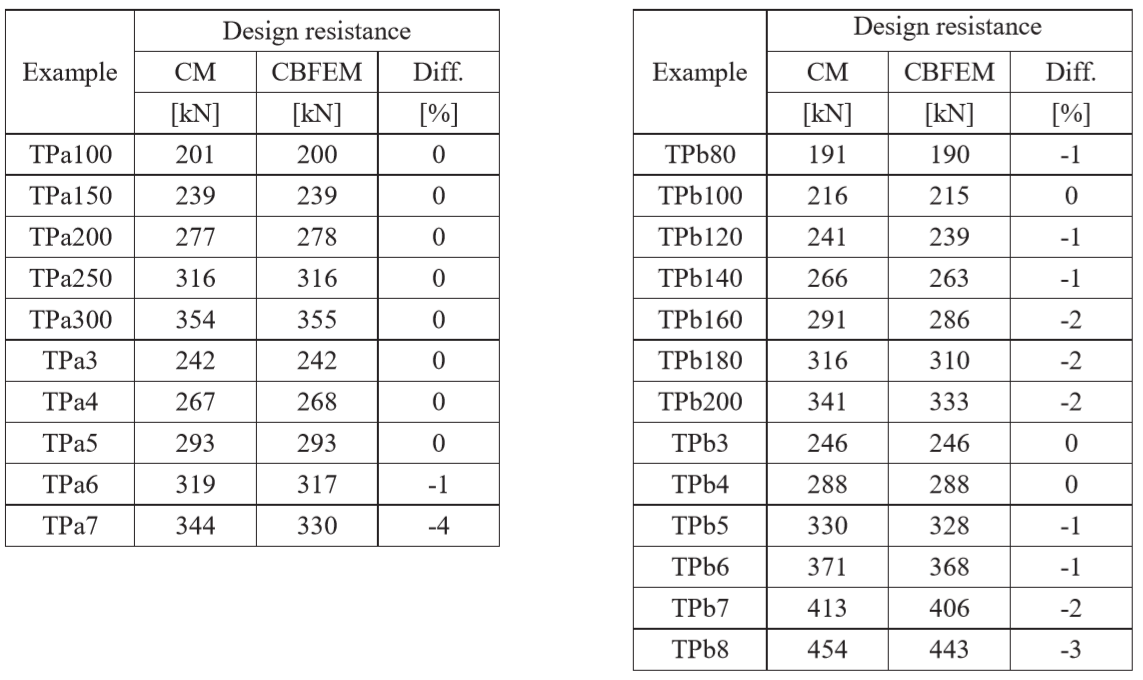
Design weld’s resistance calculated by CBFEM is compared with the results of CM. Results are presented in Tab. 4.1.2. The study is performed for two parameters length of the weld and effective throat thickness in three weld configurations, e.g. for the transverse weld, for the parallel welds, and for combination of the transverse and parallel welds.
Tab. 4.1.2 Comparison of CBFEM and CM
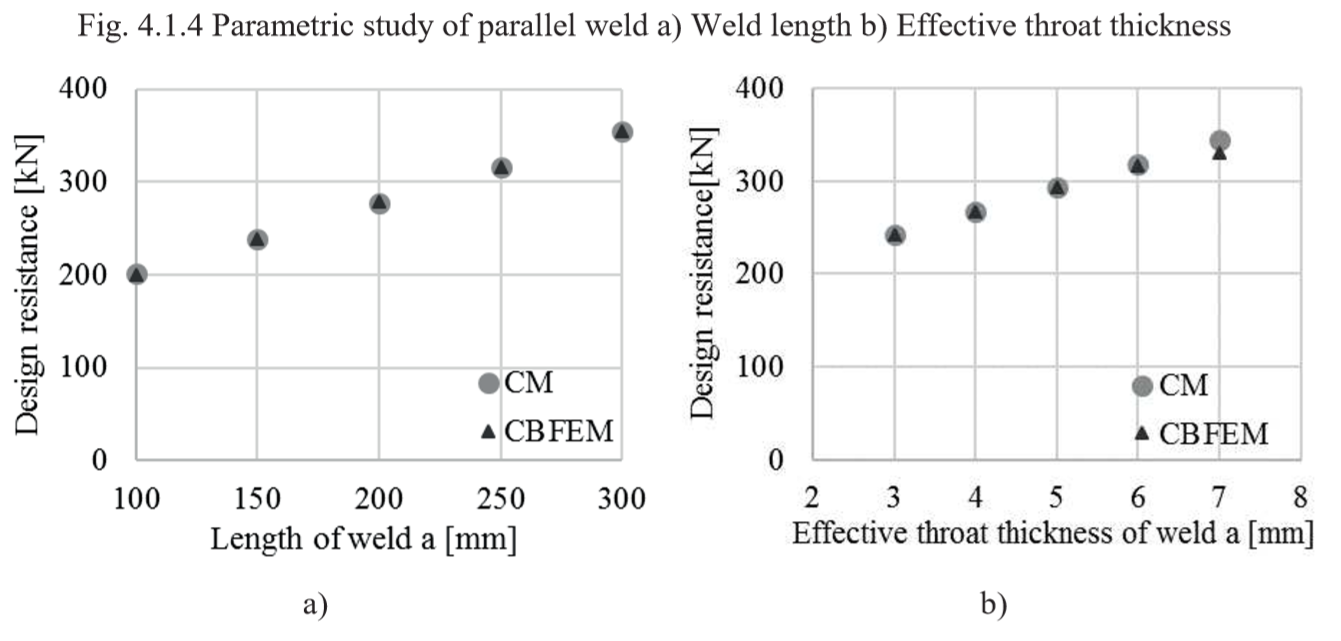
Results of CBFEM and CM are compared and sensitivity study is presented. The influence of weld length and effective throat thickness on the design resistance of the transverse weld is shown in Fig. 4.1.3. of the parallel weld in Fig. 4.1.4 and of the combination of both welds in Fig. 4.1.5. The sensitivity study shows good agreement for all weld configurations.
Fig. 4.1.3 Parametric study of transverse weld a) Weld length b) Effective throat thickness
Fig. 4.1.4 Parametric study of parallel weld a) Weld length b) Effective throat thickness
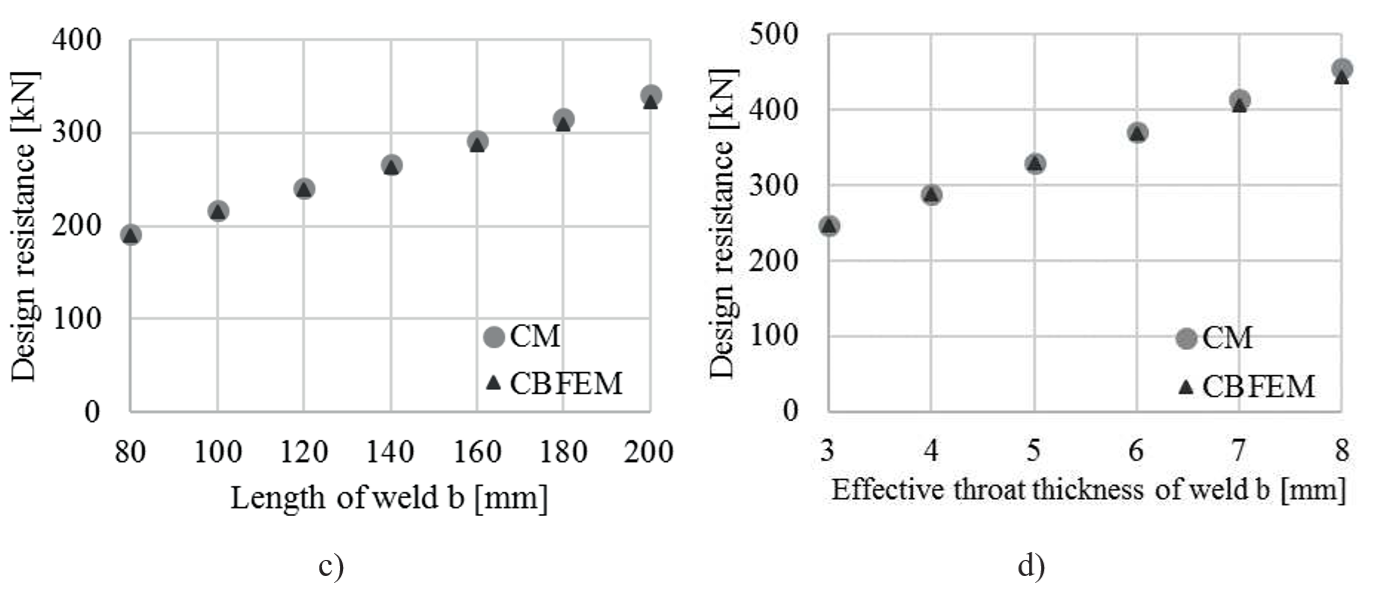
Fig. 4.1.5 Parametric study of combination of transverse and parallel weld a) Length of weld a
b) Effective throat thickness of weld a c) Length of weld b d) Effective throat thickness of weld b
To illustrate the accuracy of the CBFEM model the results of the sensitivity study are summarized in a diagram comparing CBFEM’s and CM’s design resistance, see Fig. 4.1.6. The results show that the difference of the two calculation methods is in all cases less than 10 %.
Fig. 4.1.6 Verification of CBFEM to CM
4.1.5 Benchmark
Example Inputs
Plate 1
- Thickness t1 = 20 mm
- Width b1 = 200 mm
- Steel
S235 Plate 2
- Thickness t2 = 20 mm
- Width b2 = 300 mm
- Offset ez = -20 mm
- Steel S235
Weld, parallel fillet welds see Fig. 4.1.7.
- Throat thickness ab = 3 mm
- Weld length Lb = 150 mm
Output
- Design resistance in tension FRd = 183 kN
Fig. 4.1.7 Benchmark example for the welded lap joint with parallel fillet welds